경사 하강법의 종류
1-1. 배치 경사 하강법
- 가장 기본적인 경사 하강법(Vanlilla Gradient Descent)
- 데이터셋 전체를 고려하여 손실함수를 계산함
- 한 번의 Epoch에 모든 파라미터 업데이트를 단 한번만 수행
- Batch의 개수와 Iteration은 1이고, Batch Size는 전체 데이터의 갯수
- 파라미터 업데이트할 때 한 번에 전체 데이터셋을 고려하기 때문에 모델 학습 시 많은 시간과 메모리가 필요하다는 단점이 있음
1-2. 확률적 경사 하강법
- 확률적 경사 하강법(Stochastic Gradient Descent)은 배치 경사 하강법이 모델 학습시 많은 시간과 메모리가 필요하다는 단점을 개선하기 위해 제안된 기법을 뜻함.
- Batch Size를 1로 설정하여 파라미터를 업데이트 하기 때문에 배치 경사 하강법 보다 훨씬 빠르고 적은 메모리로 학습이 진행됨.
- 파라미터 값의 업데이트 폭이 불안정하기 때문에 정확도가 낮은 경우가 생길 수 있음
1-3. 미니 배치 경사 하강법
- 미니 배치 경사 하강법(Mini-Batch Gradient Descent)은 Batch Size를 설정한 Size로 사용
- 배치 경사 하강법보다 모델 학습 속도가 빠르고, 확률적 경사 하강법보다 안정적인 장점이 있음
- 딥러닝 분야에서 가장 많은 확용되는 경사 하강법
- 일반적으로 Batch Size를 16, 32, 64, 128과 같은 2의 n제곱에 해당하는 값으로 사용하는게 보편적이였음
- 단, 지금은 그럴 필요가 없음. 예전엔 cpu로 계산을 진행하는데 누수를 방지하고자 2의 n제곱으로 사용했지만 지금은 그럴 필요가 없음.
2-1. SGD(확률적 경사 하강법)
- 매개변수 값을 조정 시 전체 데이터가 아니라 랜덤으로 선택한 하나의 데이터에 대해서만 계산하는 방법
2-2. 모멘텀(Momentum)
- 관성이라는 물리학의 법칙을 응용한 방법
- 경사 하강법에 관성을 더 해줌
- 접선의 기울기에, 한 시점 이전의 접선의 기울기값을 일정한 비율만큼 반영
2-3. 아다그라드(Adagrad)
- 모든 매개변수에 동일한 학습률(Learning rate)을 적용하는 것은 비효율적이라는 생각에서 만들어진 학습방법
- 처음에는 크게 학습하다가 조금씩 작게 학습시킴
2-4. 아담(Adam)
- 모멘텀 + 아다그라드
2-5. AdamW
- Adam optimizer의 변형
- Adam의 일부 약점(가중치 감쇠)과 성능 향상을 위해 고안
와인 품종 예측하기
※ skelarn.datasets.load_wine이라는 데이터셋을 이용하여 품종 예측
1. 필요모듈 임포트
from sklearn.datasets import load_wine
x_data, y_data = load_wine(return_X_y=True, as_frame=True)
2. x_data 값 확인
x_data.head()
3. y_data 값 확인
y_data.head()
# 결과값 =>
# 0 0
# 1 0
# 2 0
# 3 0
# 4 0
# Name: target, dtype: int64
4. x_data, y_data를 tensor로 변경 후 shape
x_data = torch.FloatTensor(x_data.values)
y_data = torch.LongTensor(y_data.values)
print(x_data.shape)
print(y_data.shape)
# 결과값 =>
# torch.Size([178, 13])
# torch.Size([178])
5. split하여 데이터 분활 후 shape
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x_data, y_data, test_size=0.2, random_state=2024)
print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)
# 결과값 =>
# torch.Size([142, 13]) torch.Size([142])
# torch.Size([36, 13]) torch.Size([36])
6. 학습
model = nn.Sequential(
nn.Linear(13, 3)
)
optimizer = optim.Adam(model.parameters(), lr=0.01)
epochs = 1000
for epoch in range(epochs + 1):
y_pred = model(x_train)
loss = nn.CrossEntropyLoss()(y_pred, y_train)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch % 100 == 0:
y_prob = nn.Softmax(1)(y_pred)
y_pred_index = torch.argmax(y_prob, axis=1)
y_train_index = y_train
accuracy = (y_train_index == y_pred_index).float().sum() / len(y_train) * 100
print(f'Epoch {epoch:4d}/{epochs}, Loss: {loss:.6f}, Accuracy: {accuracy:.2f}%')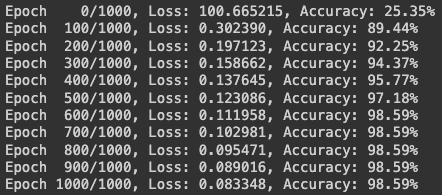
y_pred = model(x_test)
y_pred[:5]
# 결과값 =>
# tensor([[-28.7244, -30.6228, -22.7633],
# [-51.6261, -58.9351, -60.1704],
# [-17.1980, -12.4382, -12.0121],
# [-54.0891, -59.6118, -59.6391],
# [-30.0164, -31.9313, -35.4247]], grad_fn=<SliceBackward0>)
# ---------------------------------------
y_prob = nn.Softmax(1)(y_pred)
y_prob[:5]
# 결과값 =>
# tensor([[2.5695e-03, 3.8493e-04, 9.9705e-01],
# [9.9914e-01, 6.6892e-04, 1.9448e-04],
# [3.3733e-03, 3.9373e-01, 6.0290e-01],
# [9.9218e-01, 3.9641e-03, 3.8571e-03],
# [8.6818e-01, 1.2793e-01, 3.8885e-03]], grad_fn=<SliceBackward0>)
print(f'0번 품종일 확률: {y_prob[0][0]:.2f}')
print(f'1번 품종일 확률: {y_prob[0][1]:.2f}')
print(f'2번 품종일 확률: {y_prob[0][2]:.2f}')
# 결고값 =>
# 0번 품종일 확률: 0.00
# 1번 품종일 확률: 0.00
# 2번 품종일 확률: 1.00
# ----------------------------------------
y_pred_index = torch.argmax(y_prob, axis=1)
y_pred_index
# 결과값 =>
# tensor([2, 0, 2, 0, 0, 1, 2, 1, 2, 0, 1, 1, 1, 0, 1, 1, 0, 2, 0, 2, 0, 2, 1, 1,
# 1, 2, 2, 0, 2, 1, 1, 0, 0, 2, 1, 2])
# ----------------------------------------
accuracy = (y_test == y_pred_index).float().sum() / len(y_test) * 100
print(f'테스트 정확도는 {accuracy:.2f}%입니다!')
# 결과값 => 테스트 정확도는 94.44%입니다!'Study > 머신러닝과 딥러닝' 카테고리의 다른 글
| [머신러닝과 딥러닝] 17. 딥러닝(AND, OR, XOR 게이트) (1) | 2024.01.10 |
|---|---|
| [머신러닝과 딥러닝] 16. 데이터 로더(손글씨 인식 모델) (0) | 2024.01.10 |
| [머신러닝과 딥러닝] 15. 파이토치로 구현한 논리회귀_1 (0) | 2024.01.10 |
| [머신러닝과 딥러닝] 14. 파이토치로 구현한 선형회귀_2(지면온도 예측) (0) | 2024.01.09 |
| [머신러닝과 딥러닝] 14. 파이토치로 구현한 선형회귀_1 (0) | 2024.01.09 |
